逆向人学密码(二)TEA
Contents
TEA
算法简介
-
TEA:微型加密算法(Tiny Encryption Algorithm,TEA)是一种易于描述和执行的块密码,通常只需要很少的代码就可实现。
-
块密码:在密码学中,分组加密(英语:Block cipher),又称分块加密或块密码,是一种对称密钥算法。它将明文分成多个等长的模块(block),使用确定的算法和对称密钥对每组分别加密解密。
算法属性
-
TEA操作处理两个32位无符号整型上(可能源于一个64位数据)
-
TEA使用一个128位密钥
算法过程
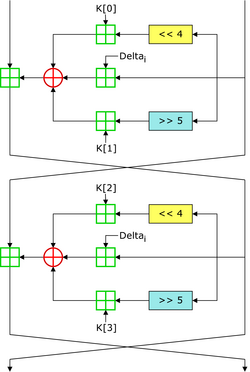
- TEA遵循Feistel网络

-
Feistel网络构造细节:
-
令F为轮函数,并令$K_0,K_1,……K_n$分别为0,1,……n的子密钥
-
将明文拆分为两个等长的块,$(L_0,R_0)$
-
对每轮$i=0,1……n$,计算
$L_{i+1}=R_i$
$R_{i+1}=L_i \bigoplus F(R_i,K_i)$
-
则密文为$(R_{n+1},L_{n+1})$
-
加解密过程唯一区别是子密钥顺序反转
-
- TEA实现过程
C语言实现
|
|
逆向算法特征
-
delta的值0x9e3779b9,且有sum在每一轮逐次累加,但delta数值容易被魔改
-
加密轮次一般为32轮,且每轮加密都是对两个32位数据进行
-
<<4与>>5及其加密逻辑一般是最重要的突破口
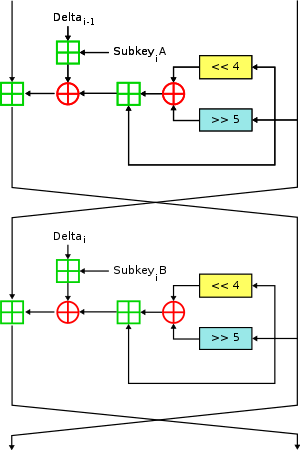
XTEA
|
|
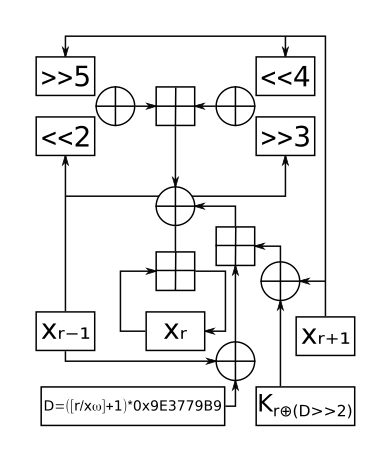
XXTEA
|
|